Financial Analysis

Candlestick Patterns: Inverted Hammer

 

The Inverted Hammer is a candlestick pattern commonly seen in technical analysis, typically at the bottom of a downtrend, indicating potential reversal or a shift in market sentiment. It is a single candlestick pattern with a specific shape and structure, often used by traders to anticipate possible bullish movements. Here’s a detailed breakdown of the Inverted Hammer:

 

---

Structure and Appearance

The Inverted Hammer has the following characteristics:

1. Small Real Body: The real body (the distance between the open and close prices) is small, which shows that the price did not move much during the trading session. The body can be either at the top or the bottom of the candlestick.
2. Long Upper Shadow: The key feature of the Inverted Hammer is its long upper shadow (or wick). This represents a sharp price movement to the upside that was not sustained, signaling that buyers pushed the price higher during the session but were ultimately overpowered by sellers who drove the price back down.
3. Little or No Lower Shadow: Ideally, there is little or no lower shadow, although a tiny lower wick is permissible. This suggests that there was little price action on the downside during the session.
4. Close Near the Low: The close should be relatively close to the open, and ideally near the bottom of the candlestick, to show that the sellers managed to regain control by the end of the trading period.

 

---

Interpretation of the Inverted Hammer

• Location is Key: The Inverted Hammer pattern is most significant when it appears at the bottom of a downtrend. It signals a potential reversal, indicating that despite the prevailing downward trend, the buyers are starting to assert themselves, and a change in direction may be coming.
• Bullish Reversal Signal: The Inverted Hammer suggests that during the trading session, buyers pushed the price higher (long upper shadow), but sellers regained control, causing the price to close near the open. Despite this, the long upper shadow shows that the buying pressure is present and could be an indication that the market is preparing for a bullish reversal.

 

---

How to Trade the Inverted Hammer

1. Confirmation: The Inverted Hammer alone does not guarantee a reversal. Traders typically look for confirmation in the form of a bullish candlestick that follows it (such as a strong white or green candle) to validate that the market is truly reversing.
2. Volume: Higher volume during the formation of the Inverted Hammer increases its reliability. If the price action of the hammer is accompanied by rising volume, it indicates stronger conviction in the market reversal.
3. Stop-Loss and Targets: Traders often place a stop-loss just below the low of the Inverted Hammer pattern, in case the reversal does not materialize. The target for this pattern would often be the next significant resistance level or a certain percentage gain from the entry point.

 

---

Inverted Hammer vs. Shooting Star

The Inverted Hammer looks similar to the Shooting Star candlestick, but the key difference is their location:

• Inverted Hammer appears in a downtrend and signals a potential reversal to the upside.
• Shooting Star appears in an uptrend and signals a potential reversal to the downside.

While they share a similar structure, their implications differ based on the prevailing market trend.

 

Example

Imagine a stock that has been in a downtrend for several weeks. On one particular day, the price opens at $50, moves up to $55, and then closes back at $50. The candle formed would have a small body near the bottom of the candle and a long upper shadow, creating an Inverted Hammer. This suggests that buyers tried to push the price higher, but sellers regained control. If the next day shows a strong bullish candlestick, traders may interpret this as a signal to go long, anticipating the start of an upward trend.

 

---

Limitations

• False Signals: As with all candlestick patterns, the Inverted Hammer is not foolproof. It can give false signals, especially if there’s no confirmation candle or if it occurs in a strong downtrend without any clear sign of reversal.
• Context Matters: The pattern is more reliable when combined with other technical indicators, such as RSI (Relative Strength Index), moving averages, or support and resistance levels, rather than relying solely on the candlestick pattern.

 

---

Conclusion

The Inverted Hammer is a useful candlestick pattern that signals potential bullish reversal when it appears at the bottom of a downtrend. It highlights a shift in market sentiment, where buyers begin to show strength despite the prevailing bearish trend. However, for increased reliability, the pattern should be followed by a confirmation of upward movement, and traders should always consider the broader context and other indicators.

 

Engulfing (Bearish)

 

Indication

Bearish reversal

 

Reliability

Medium

 

Description

Occurring during an uptrend, this pattern characterized by a large black real body, which engulfs a white real body (it doesn’t need to engulf the shadows). This signifies that the uptrend has been hurt and the bears may be gaining strength. The Engulfing indicator is also the first two candles of the Three Outside patterns.
It is a major reversal signal.

Factors that are increasing this signal’s reliability:

1. The first candlestick has a very small real body and the second candlestick a very large real body.
2. The pattern appears after a protracted or very fast move.
3. Heavy volume on the second black candlestick.
4. The second candlestick engulfs more than one real body.

 

Notes

• Two candle Bearish pattern
• Reverse of a bullish engulfing pattern
• Must come after and uptrend
• High of the pattern becomes resistance
• First candle is white real body
• Second candle is a black body that completely engulfs the first candle
• The first candle real body must be as small as possible
• Shadows are not a concern

Engulfing (Bullish)

 

Coming soon…

Shooting Star

 

Notes

• Single candle
• Bearish pattern
• Inverse of a hammer
• More powerful than the hammer
• Colour of the body does not matter
• Must come after an uptrend
• Long upper shadow must be at least twice the height of the real body
• Works better compared to hammer
• High of the pattern is the resistance
• Resistance is usually tested less frequently
• The real body must be as small as possible
• The lower shadow must be as small as possible

Candlestick Patterns: Hammer

 

 

Summary

 

Candlestick	Details
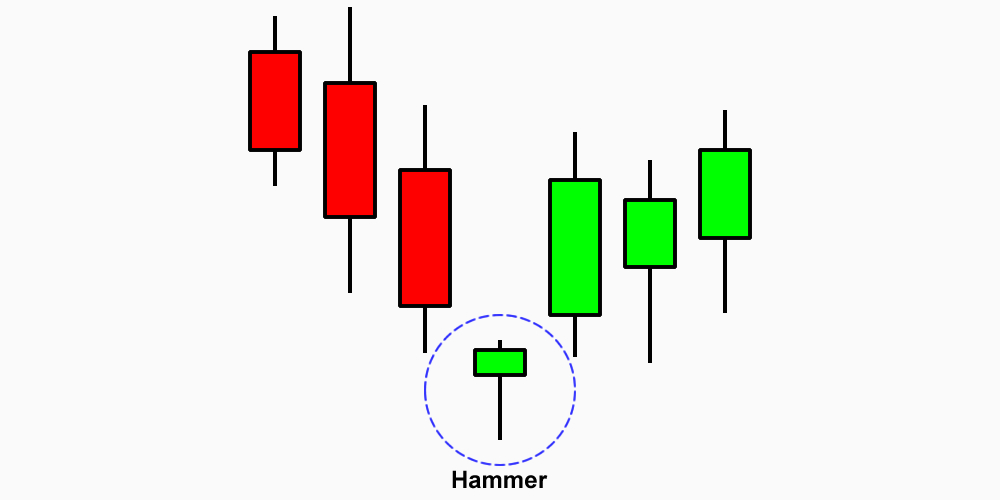
Pattern:	Hammer
Type:	Reversal
From:	Downward Trend / Bearish (-)
To:	Upward Trend / Bullish (+)
Position:	Long (Buy)

 

The Hammer candlestick pattern is one of the most well-known reversal patterns in technical analysis. It can signal a potential change in trend direction, particularly when it forms after a downtrend. The Hammer is important because it suggests that the market is attempting to reject lower prices, and it often indicates a shift in market sentiment from bearish to bullish.

 

---

What is a Hammer Candlestick?

The Hammer is a single candlestick pattern that has the following characteristics:

• Small body: The real body (the area between the open and close) is small, and it can either be bullish (close > open) or bearish (close < open). However, the color of the body is not as critical in the Hammer pattern.
• Long lower shadow: The lower shadow (the line below the body) is at least twice the length of the body, and it can be even longer. This long lower shadow indicates that the price was pushed lower during the session but closed near the opening price, suggesting that the bears lost control.
• Short or no upper shadow: The upper shadow (the line above the body) is either very short or nonexistent. This shows that the price did not reach significantly higher levels during the session.

 

When these conditions are met, it forms the Hammer candlestick. The pattern typically appears at the bottom of a downtrend and can signal a potential reversal or a shift in market sentiment.

 

---

Key Features of the Hammer

• Shape: A small body with a long lower shadow and a very short or nonexistent upper shadow.
• Location: Most often found at the bottom of a downtrend (although it can also appear after a consolidation or a period of indecision).
• Price Action: The long lower shadow indicates that the bears were initially in control, but the bulls managed to push the price back up toward the open, resulting in a close near the opening price.

 

---

How to Interpret the Hammer Candlestick Pattern

• Rejection of Lower Prices: The long lower shadow reflects that during the trading session, sellers (bears) tried to push the price lower, but by the close, buyers (bulls) managed to bring the price back up. This can indicate a shift in momentum and a potential reversal from a downtrend to an uptrend.
• Psychological Significance: The Hammer suggests that the market tried to go lower (bears dominated early), but the strength of the buyers emerged to push the price back up, showing that the selling pressure may have exhausted itself. The candle indicates a potential change in sentiment, as the buyers take control.
• Confirmation Needed: Although the Hammer is a strong reversal signal, it is not a guarantee. To increase the reliability of the signal, traders often look for confirmation from the next candlestick or other indicators. A bullish confirmation could be a bullish engulfing, a gap up, or a continuation pattern after the Hammer.

 

---

Types of Hammer Patterns

1. Regular Hammer: A small body with a long lower shadow and little or no upper shadow, typically appearing at the bottom of a downtrend. This is the classic form of the Hammer pattern.
2. Inverted Hammer: An inverted Hammer looks similar to the regular Hammer but with a long upper shadow and a small body near the bottom of the candlestick. While it’s also a potential reversal pattern, it tends to be more common after a downtrend has already ended, signaling a possible continuation or shift toward an uptrend.

 

---

How to Trade the Hammer Candlestick Pattern

1. Location of the Hammer: For a Hammer to be considered a potential reversal, it should appear after a significant downtrend. The longer the downtrend, the stronger the reversal signal could be.
2. Entry Point:
   • A common entry point is to wait for confirmation in the form of the next candlestick. If the next candle closes above the high of the Hammer, this is considered confirmation that the market is shifting from bearish to bullish, and it might be a good time to enter a long (buy) position.
   • Alternatively, traders might enter at the break of the Hammer’s high, expecting the reversal to continue.
3. Stop Loss: A logical stop loss is typically placed just below the low of the Hammer candle. This protects the trader if the market doesn’t reverse as expected and continues to fall.
4. Target: Traders often aim for a return to the previous resistance levels or a price target based on the trader’s risk-reward ratio. The target can also be a key moving average, Fibonacci level, or previous highs.

 

---

Example of the Hammer Candlestick in Action

Imagine a stock has been in a downtrend, consistently moving lower day by day. On one particular day, the stock opens at $50, falls to $45 during the trading session (forming the long lower shadow), but then rebounds and closes at $49. This forms a Hammer candlestick. The price action shows that, despite initial selling pressure, buyers managed to push the price back up to close nearly where the price opened.

If, the next day, the price opens above $49 and continues to move higher, this would serve as confirmation that the market sentiment may have shifted from bearish to bullish. A trader could then enter a long position, placing a stop loss just below $45 (the low of the Hammer), targeting a return to higher levels.

 

---

Confirmation and Risk Management

• Confirmation Candlestick: It’s crucial to wait for a confirmation candle to validate the Hammer pattern. A confirmation candle is usually a bullish candle that closes above the high of the Hammer, showing that the reversal is gaining momentum.
• Volume: High volume accompanying the formation of the Hammer is a positive sign, as it confirms that the buyers are willing to step in after the price falls to a low level.
• Market Context: The Hammer should be interpreted in the context of the broader market or trend. A Hammer in a sideways or uptrend might not have the same significance as one that appears after a prolonged downtrend.

 

---

Limitations of the Hammer Pattern

• False Signals: The Hammer is not foolproof and can give false signals, especially in markets that are in a strong trend. If the market does not follow through with a reversal and continues lower, the pattern might fail.
• Preceding Trend: The Hammer is most reliable when it follows a clear downtrend. If the market is consolidating or moving sideways, a Hammer can sometimes signal indecision rather than a clear reversal.
• Over-reliance: Relying solely on the Hammer candlestick without confirming signals or additional analysis can lead to poor trading decisions. Combining the Hammer with other tools (e.g., trendlines, oscillators, support/resistance levels) can improve accuracy.

 

---

Summary

• The Hammer is a single candlestick pattern characterized by a small body, a long lower shadow, and a short or no upper shadow.
• It usually appears at the bottom of a downtrend, signaling potential bullish reversal.
• The long lower shadow indicates that sellers tried to push the price lower, but buyers stepped in to push the price back up, showing a shift in market sentiment.
• Confirmation from the next candle, volume, and broader market context are key to enhancing the reliability of the signal.
• Traders typically enter a long position after a confirmation candle, placing a stop loss just below the low of the Hammer.

Understanding the Hammer pattern, along with its nuances, can significantly improve your ability to spot potential reversals and make informed trading decisions.

 

The Basics

The Basics

Forecasting

Moving Average (MA)

 

Step 1: Select the ‘Data’ tab.

 

 

Step 2: Click on ‘Data Analysis’.

 

 

Step 3: Select ‘Moving Average’.

Step 4: Click ‘OK’.

 

 

Step 5: Enter the ‘Input Range’.

Step 6: Check ‘Labels in First Row’ (if applicable).

Step 7: Enter the ‘Interval.’

Step 8: Enter the ‘Output Range’.

Step 9: Check the ‘Chart Output’ box (optional).

Step 10: Check the ‘Standard Errors’ box (optional).

Step 11: Click ‘OK’.

 

 

 

Date	S&P/ASX 200	MA5
2020-09-07	5944.80
2020-09-08	6007.80
2020-09-09	5878.60
2020-09-10	5908.50
2020-09-11	5859.40	5919.82
2020-09-14	5899.50	5910.76
2020-09-15	5894.80	5888.16
2020-09-16	5956.10	5903.66
2020-09-17	5883.20	5898.60
2020-09-18	5864.50	5899.62
2020-09-21	5822.60	5884.24
2020-09-22	5784.10	5862.10
2020-09-23	5923.90	5855.66
2020-09-24	5875.90	5854.20
2020-09-25	5964.90	5874.28
2020-09-28	5952.30	5900.22
2020-09-29	5952.10	5933.82
2020-09-30	5815.90	5912.22
2020-10-01	5872.90	5911.62
2020-10-02	5791.50	5876.94

 

Simple Interest

Notes

 

---

Formula

 

---

Calculator