

When you run a regression analysis in Excel (via the Data Analysis Toolpak), it provides you with several key sections of output:
Each of these components helps assess how well the regression model fits your data and gives you insights into the relationship between the dependent and independent variables.
Let’s go through each section in detail:
The Regression Statistics section summarizes key metrics about the regression model. The most important pieces here include R-squared, Multiple R, and the Standard Error.
The ANOVA Table assesses the overall significance of the regression model. It breaks down the variation in the dependent variable into components explained by the model and unexplained (error).
The Coefficients Table shows the values of the regression coefficients, which are the estimated parameters for the regression equation. These coefficients tell you how each independent variable (predictor) influences the dependent variable.
Residuals are the differences between the observed data points and the values predicted by the model. Analyzing residuals helps you evaluate how well the model fits the data.
With all these components, you can thoroughly assess the performance and reliability of your regression model and ensure that it provides meaningful insights.
| Uppercase | Lowercase | Name |
|---|---|---|
| Α | α | alpha |
| Β | β | beta |
| Γ | γ | gamma |
| Δ | δ | delta |
| Ε | ε | epsilon |
| Ζ | ζ | zêta |
| Η | η | êta |
| Θ | θ | thêta |
| Ι | ι | iota |
| Κ | κ | kappa |
| Λ | λ | lambda |
| Μ | μ | mu |
| Ν | ν | nu |
| Ξ | ξ | xi |
| Ο | ο | omikron |
| Π | π | pi |
| Ρ | ρ | rho |
| Σ | σ, ς | sigma |
| Τ | τ | tau |
| Υ | υ | upsilon |
| Φ | φ | phi |
| Χ | χ | chi |
| Ψ | ψ | psi |
| Ω | ω | omega |
| Parameter | Description |
|---|---|
| S0 | spot price at inception of the contract (t=0) |
| FP | forward price |
| Rf | annual risk-free rate |
| T | forward contract term (years) |
Mark-to-market is an accounting practice or process that involves adjusting the value of an asset or a liability to reflect its current market value rather than its book value or historical cost. The goal of MTM is to ensure that financial statements reflect the true current value of assets and liabilities as determined by the latest market prices.
In the context of futures contracts, MTM refers to the daily process of revaluing the contract based on the market’s closing price and adjusting the margin accounts of the involved parties accordingly.
Mark-to-market is not limited to futures markets—it also applies to a range of other financial assets, including:
Let’s say a trader enters into a long futures contract on oil with a price of USD 70 per barrel. Here’s how MTM would work:
Each day, the trader’s margin account is adjusted according to the daily change in the contract’s value, ensuring that the position is fully collateralized and reflecting the real-time market value of the contract.
Mark-to-market is an essential process for ensuring that the values of financial contracts, particularly in futures markets, are accurately and transparently reflected based on current market conditions. It helps to manage risk, ensure liquidity, and provide up-to-date financial reporting, all while preventing large-scale losses or defaults. The MTM system of daily settlement and revaluation promotes efficiency and stability in financial markets.
A risk premium is the additional return or yield that an investor requires for taking on the extra risk associated with an investment compared to a risk-free alternative. In other words, it compensates investors for bearing uncertainty or potential losses that come with riskier assets.
The formula for the Risk Premium is generally expressed as the difference between the expected return on a risky asset and the return on a risk-free asset. Here’s the formula:
Risk Premium = Expected Return on Risky Asset − Risk-Free Rate
Where:
Example:
If the expected return on a corporate bond is 6%, and the risk-free rate (say, the return on a 1-year Treasury bond) is 2%, the risk premium would be:
This means that investors require an additional 4% return for taking on the risk of the corporate bond, as compared to the risk-free Treasury bond.
In these cases, the formula follows the same basic structure but is applied to different assets (stocks, corporate bonds, etc.).
The difference between the return on a risky asset and the return on a risk-free asset is the risk premium.
Let’s say the risk-free rate (the return on a 1-year U.S. Treasury bond) is 2%, and you’re considering investing in a corporate bond with a higher risk of default. If the expected return on the corporate bond is 5%, the risk premium for this bond would be 5% – 2% = 3%.
In the context of the Unbiased Expectation Hypothesis, if there were a risk premium in play, long-term interest rates would no longer be an unbiased reflection of future short-term rates. Instead, long-term rates would also incorporate a premium for the risk of holding longer-term securities. This would make the relationship between short-term and long-term rates more complex, as investors would be demanding a premium to compensate for the uncertainty over time.
In summary, the risk premium is a fundamental concept in finance, representing the extra return investors demand to compensate for the risks they assume when investing in assets that are not risk-free.
The formula for the present value with discrete compounding is:
$$PV=\frac{FV}{\left( 1+\frac{r}{n} \right)^{nt}}$$
Where:
This formula calculates the present value of a future cash flow, discounted at an interest rate r, with n compounding periods per year, over a period of t years.
The formula for the present value with continuous compounding is:
$$PV=FV⋅e^{−𝑟𝑡}$$
Where:
This formula calculates the present value of a future cash flow when interest is compounded continuously at a rate r over time t.
The given formula is:
$$F_{0}(T) = S_{0}*(1+r)^T$$
To solve for
, we can follow these steps:
(1) Divide both sides of the equation by
:
$$\frac{F_{0}(T)}{S_{0}} = (1+r)^T$$
(2) Take the natural logarithm (ln) of both sides:
$$ln\left( \frac{F_{0}(T)}{S_{0}} \right) = ln\left( (1+r)^T \right)$$
(3) Use the logarithmic identity
:
$$ln\left( \frac{F_{0}(T)}{S_{0}} \right) = T*ln(1+r)$$
Finally, solve for
by dividing both sides by
:
$$T=\frac{ln\left( \frac{F_{0}(T)}{S_{0}} \right)}{ln(1+r)}$$
So the formula to find T is:
$$T=\frac{ln\left( \frac{F_{0}(T)}{S_{0}} \right)}{ln(1+r)}$$
xxx
A Collar (also known as a Protective Collar) is a popular options strategy that combines the use of a long position in the underlying asset, a covered call, and a protective put. The purpose of a collar is to limit potential losses on the underlying asset while also capping potential gains. This strategy is often used by investors who want to protect themselves from downside risk, but who are also willing to limit their upside potential in exchange for that protection.
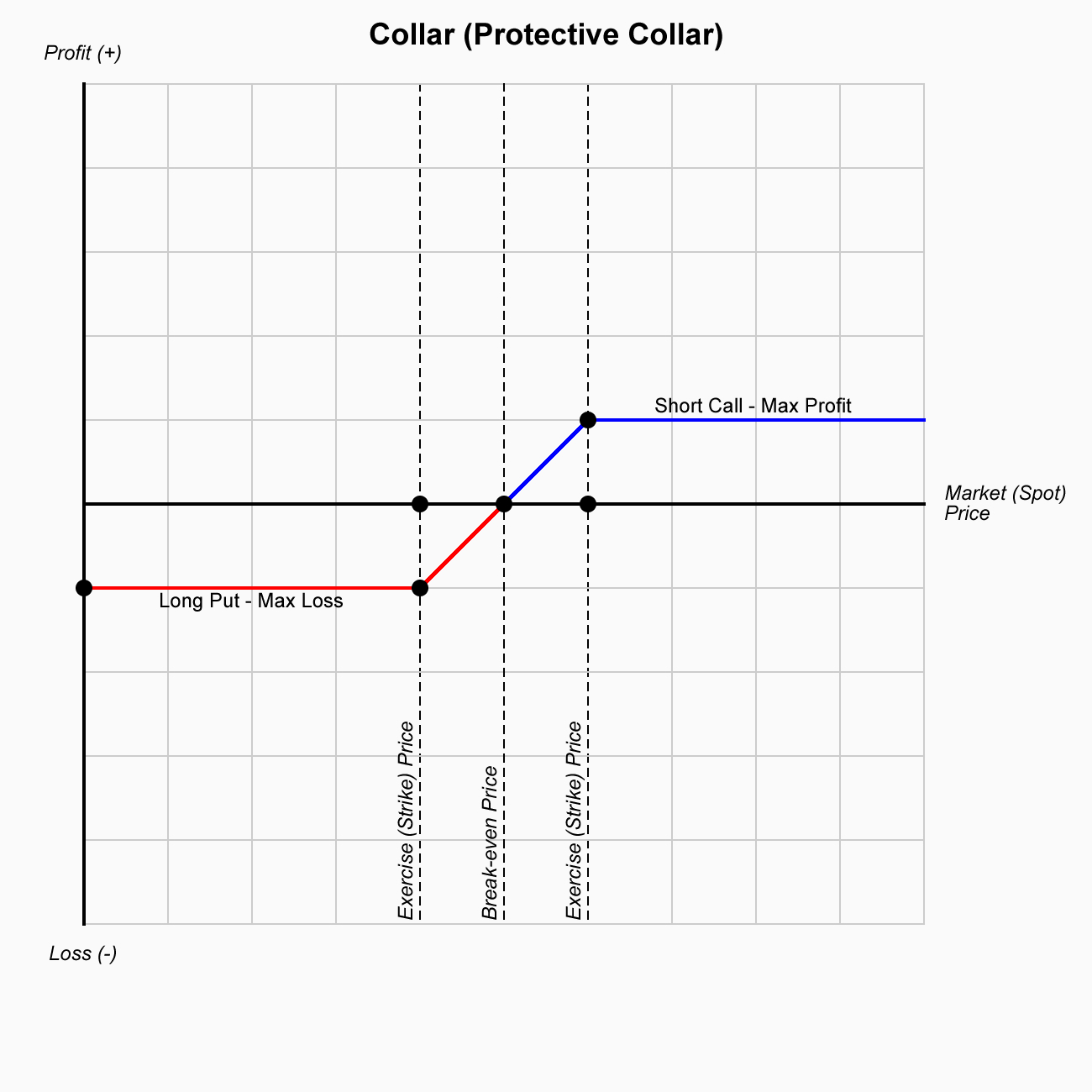
The collar strategy is used to limit downside risk while also capping upside potential. This strategy is suitable for investors who want to protect their gains or limit losses in a volatile or uncertain market but are willing to forgo unlimited potential profits in return for the protection provided by the put option.
The collar strategy typically involves the following steps:
The protective collar limits both potential losses (through the protective put) and potential gains (through the sold call option). The cost of buying the protective put is partially or fully offset by the premium received from selling the call option, making it an affordable risk management strategy for some investors.
Let’s consider an investor who owns 100 shares of a stock currently trading at $50 per share. The investor wants to limit potential losses but also wants to potentially profit from some upside movement. The investor decides to implement a collar strategy by selling a covered call and buying a protective put.
In this case, the investor is using the $200 premium from the covered call to help offset the cost of the $100 premium for the protective put. Therefore, the net cost of the collar strategy is $100 ($200 premium from the call minus $100 cost of the put).
The collar (protective collar) strategy is a risk management tool that allows investors to protect against downside risk while capping potential upside gain. By combining a long position in the asset, selling a covered call, and buying a protective put, the collar provides a defined risk/reward profile. This strategy is useful for investors looking to hedge their positions in volatile markets, protect gains, or generate income through options premiums, while also being willing to limit potential profits. The strategy works well in markets with uncertainty or volatility and is especially attractive to investors with neutral to slightly bullish outlooks.
A Cash-Secured Put is an options trading strategy that involves selling a put option while setting aside sufficient cash to purchase the underlying asset (if the put option is exercised). This strategy is commonly used by investors who are willing to buy the underlying asset at a certain price (the strike price of the put) in exchange for receiving an upfront premium from selling the put option.
This strategy is considered conservative and is typically employed when an investor has a neutral to slightly bullish outlook on the underlying asset and is looking to generate income through premiums while potentially acquiring the asset at a price lower than its current market value.
The main goal of a cash-secured put is to generate income from the premium received from selling the put option while keeping the possibility of acquiring the underlying asset at a discount (the strike price) if the option is exercised. It is used in scenarios where the investor is willing to buy the asset at the strike price but is also content with keeping the premium if the option expires worthless.
The maximum profit occurs when the put option expires worthless (i.e., the price of the underlying asset remains above the strike price). In this case, the investor keeps the full premium received for selling the put option as profit.
Mathematically:
Maximum Loss
The maximum loss occurs if the price of the underlying asset falls to zero. In this case, the investor would have to buy the asset at the strike price, which would result in a significant loss. However, this loss is partially offset by the premium received from selling the put option.
Mathematically:
Breakeven Point
The breakeven point is the price at which the investor will neither make a profit nor a loss. It occurs when the price of the underlying asset is equal to the strike price minus the premium received.
Mathematically:
Example
Let’s say an investor is interested in selling a cash-secured put on a stock currently trading at $50. The investor decides to sell a put option with a strike price of $45, expiring in one month, and receives a premium of $2 per share.
Outcomes
Pros
Cons
Example Summary
A cash-secured put is a relatively conservative strategy used to generate income through the premium received from selling put options, while also providing the opportunity to acquire the underlying asset at a discount if the option is exercised. The strategy is best suited for investors with a neutral to bullish outlook who are willing to own the asset at the strike price and are looking to generate income in a stable or slightly bullish market. The maximum risk is limited to the strike price of the put minus the premium received, and the maximum profit is limited to the premium received.
A Cash-Secured Call (also known as a Cash-Backed Call) is a conservative options trading strategy that involves selling a covered call while having sufficient cash or liquid assets set aside to buy the underlying asset if the call is exercised. It’s similar to a covered call but instead of owning the underlying asset, the trader sets aside cash as collateral in case they need to buy the asset.
This strategy is typically used when the investor has a neutral to slightly bullish outlook on the underlying asset and aims to generate income from the premium received by selling the call option. The main difference between a cash-secured call and a standard covered call is that the cash-secured call does not require the investor to already own the underlying asset but instead uses cash to guarantee the potential purchase of the asset.
The objective of a cash-secured call is to generate income through the premiums received from selling the call option while maintaining the ability to purchase the underlying asset if the call is exercised. It’s a neutral to slightly bullish strategy that allows an investor to earn money in a relatively flat or mildly rising market, without having to own the underlying asset in advance.
Maximum Profit
The maximum profit in a cash-secured call strategy is limited to the premium received from selling the call option. Even if the price of the underlying asset rises significantly, the maximum profit is capped at the strike price plus the premium received.
Mathematically:
Maximum Loss
The maximum loss occurs if the price of the underlying asset falls to zero. This is because the trader still holds the cash-secured position but has no offsetting premium income (if the option expires worthless and the asset becomes worthless).
However, because the trader has set aside the cash to buy the asset, the maximum loss is limited to the full price of purchasing the underlying asset at the strike price (which would occur if the call is exercised).
Mathematically:
Breakeven Point
The breakeven point is the price at which the investor will not make a profit or loss from the strategy. It is calculated by taking the strike price of the call and subtracting the premium received from selling the call option.
Mathematically:
Example
Let’s assume a stock is currently trading at $50, and you want to sell a cash-secured call on this stock:
Outcomes
Risk/Reward Profile
Pros
Cons
Example Summary
Aside Cash: $5,500 to buy the stock if exercised
A cash-secured call is a conservative options strategy that generates income through the premiums received from selling call options while setting aside cash to cover the potential purchase of the underlying asset if the option is exercised. It is best used in a neutral to slightly bullish market, where the investor expects little movement or slight appreciation in the asset’s price. The strategy offers limited risk, as the cash set aside can be used to purchase the asset if necessary, but the profit potential is capped at the premium received.
Buying Index Puts is a straightforward and popular options trading strategy used by investors who have a bearish outlook on an underlying stock index. In this strategy, the investor buys a put option on an index (such as the S&P 500, Nasdaq-100, or other indices), which gives the buyer the right, but not the obligation, to sell the underlying index at a specific strike price before or on the expiration date of the option.
The primary goal of buying index puts is to profit from a decline in the value of the underlying index, with the benefit of limited risk. If the index falls significantly below the strike price, the investor can either exercise the put (if the option is in the money) or sell the option to lock in profits.
The objective of buying an index put is to profit from a decline in the value of the underlying index. If the index falls below the strike price of the put option, the option becomes in the money, and the investor can sell the option at a profit or exercise the option to sell the index at a higher price than its current market value.
In simpler terms, buying an index put allows an investor to bet on a decrease in the market or a specific sector represented by the index. If the market falls, the value of the put option increases, potentially resulting in profits.
Maximum Profit
Mathematically:
Maximum Loss
Mathematically:
Breakeven Point
The breakeven point is the index level at which the gains from the put option exactly offset the premium paid. It occurs when the value of the index is equal to the strike price minus the premium paid.
Mathematically:
Example
Let’s say the S&P 500 is currently trading at 4,000, and you expect the index to decline in the next month. Here’s how you might execute a buying index put strategy:
Outcomes
Risk/Reward Profile
When to Buy
Pros
Cons
Example Summary
Buying index puts is a bearish options strategy used to profit from a decline in the value of an underlying index. It offers limited risk (the premium paid) and the potential for unlimited profit if the index falls significantly. This strategy is useful for speculating on market declines, hedging existing positions, or capitalizing on market volatility. However, the strategy requires careful timing, as the option’s value erodes over time, and the investor must anticipate a significant move before expiration to realize a profit.