

Last Updated on 2021-01-30 by Admin
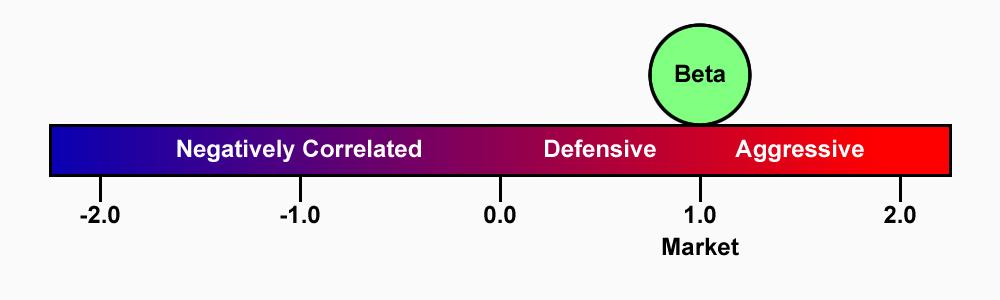
The Beta Coefficient measures the volatility of a particular share (systematic risk) in comparison to the market (unsystematic risk). It describes the sensitivity of a security’s returns in response to swings in the market.
Systematic risk is the underlying risk that affects the entire market. Large changes in macroeconomic variables, such as interest rates, inflation, GDP, or foreign exchange, are changes that impact the broader market and that cannot be avoided through diversification. The Beta coefficient relates ‘the market’ systematic risk to ‘stock-specific’ unsystematic risk by comparing the rate of change between ‘the market’ and ‘stock-specific’ returns.
Statistically, beta represents the slope of the line through a regression of data points from an individual stock’s returns against those of the market.
The beta calculation is used to help investors understand whether a stock moves in the same direction as the rest of the market, and how volatile or risky it is compared to the market.
For beta to provide any insight, the ‘market’ used as a benchmark should be related to the stock.
For example, calculating a bond ETF’s beta by using the S&P 500 as the benchmark isn’t helpful because bonds and stocks are too dissimilar. The benchmark or market return used in the calculation needs to be related to the stock because an investor is trying to gauge how much risk a stock is adding to a portfolio.
A stock that deviates very little from the market doesn’t add a lot of risk to a portfolio, but it also doesn’t increase the theoretical potential for greater returns.
The beta of the market portfolio is always 1.0
$$ Beta\;Coefficient\;(β) = \left [Covariance (rp, rb) \over Variance (rb) \right ]$$